hghjghgjjjjjjjjjjjjjjjjjjjjjjjjjj
Блог вчителя математики Дергачівської вечірньої школи Карайко Надії Миколаївни
суботу, 8 квітня 2017 р.
пʼятницю, 7 квітня 2017 р.
Уроки для дистанційної освіти
1.Определение тригонометрических функций и их свойства.
2.Четность, нечетность и периодичность тригонометрических функций.
3. Тригонометрические функции, их графики и свойства.
4.Корень n-й степени. Действия с корнями n-й степени.
понеділок, 3 квітня 2017 р.
Термін "математика" та її періодизація
Слово «математика» походить від грец. μάθημα (мàтема), що означає «пізнання» чи «вивчення»; математик, грец. μαθηματικός (математикóс), — «людина, охоплена жадобою пізнання». Математика первісно виникла як один із напрямків пошуку істини (у грецькій філософії) у сфері просторових відношень (землеміряння — геометрії) та обчислень (арифметики), для практичних потреб людини рахувати, обчислювати, вимірювати, досліджувати форми та рух фізичних тіл. Нині цей термін позначає цілком визначену область знань, пов'язану із дослідженням задач про кількість, просторові форми, процеси розвитку та формальні структури, в основі якого лежать точні означення та строгі дедуктивні методи.
Історію математики можна поділити на чотири періоди.
У перший період (приблизно 6-5 ст. до н.е.) сформувалося поняття цілого числа, раціонального дробу, віддалі, площі, об’єму, створено правила дій з числами, найпростіші правила визначення площ фігур та об’ємів тіл. Так накопичився матеріал, що склався в арифметику. Вимірювання площ і об’ємів сприяло розвиткові геометрії. На базі створення методів арифметичних обчислень зародилась алгебра, а в зв’язку з запитами астрономії – тригонометрія. Однак у цей період математика не була ще дедуктивною наукою, вона складалась переважно з прикладів на розв’язування окремих задач, у кращому разі являла собою збірку правил для їх розв’язування.
У другий період (до серед. XVII ст.) математика стає самостійною наукою з своєрідним, чітко вираженим методом і системою основних понять. В Індії було створено десяткову систему числення, в Китаї – метод розв’язування лінійних рівнянь з двома і трьома невідомими; створена стародавніми греками система викладу елементарної геометрії стала зразком дедуктивної побудови математичної теорії набагато століть вперед. У цей період з арифметики поступово виділяється теорія чисел. Велике значення мали праці Піфагора Самоського, Гіппократа Хіоського, Евдокса Кнідського, Евкліда, Архімеда, Діофанта. У Київській Русі математична освіта була на рівні найкультурніших країн Європи того часу.
Третій період (до початку ХХ ст.), в який було створено математику змінних величин, – істотно новий період у розвитку математики.
Четвертий – сучасний період - характеризується систематичним вивченням можливих типів кількісних відношень і просторових форм.
Історію математики можна поділити на чотири періоди.
У перший період (приблизно 6-5 ст. до н.е.) сформувалося поняття цілого числа, раціонального дробу, віддалі, площі, об’єму, створено правила дій з числами, найпростіші правила визначення площ фігур та об’ємів тіл. Так накопичився матеріал, що склався в арифметику. Вимірювання площ і об’ємів сприяло розвиткові геометрії. На базі створення методів арифметичних обчислень зародилась алгебра, а в зв’язку з запитами астрономії – тригонометрія. Однак у цей період математика не була ще дедуктивною наукою, вона складалась переважно з прикладів на розв’язування окремих задач, у кращому разі являла собою збірку правил для їх розв’язування.
У другий період (до серед. XVII ст.) математика стає самостійною наукою з своєрідним, чітко вираженим методом і системою основних понять. В Індії було створено десяткову систему числення, в Китаї – метод розв’язування лінійних рівнянь з двома і трьома невідомими; створена стародавніми греками система викладу елементарної геометрії стала зразком дедуктивної побудови математичної теорії набагато століть вперед. У цей період з арифметики поступово виділяється теорія чисел. Велике значення мали праці Піфагора Самоського, Гіппократа Хіоського, Евдокса Кнідського, Евкліда, Архімеда, Діофанта. У Київській Русі математична освіта була на рівні найкультурніших країн Європи того часу.
Третій період (до початку ХХ ст.), в який було створено математику змінних величин, – істотно новий період у розвитку математики.
Четвертий – сучасний період - характеризується систематичним вивченням можливих типів кількісних відношень і просторових форм.
Август Фердінанд Мебіус
17 листопада 1790 року народився відомий німецький математик і астроном Авуст Фердінанд Мебіус.
Освіту здобув у Лейпцігському університеті. де навчався впродовж 1809-1813 років. Під керівництвом видатного математика К. Гаусса вивчав астрономію у Геттінгеському університеті (1813-18140,. У 1816 році став професором У Лепцігському університеті та директором астрономічної обсерваторії у Лейпцізі. Основні праці Мебіуса присвячені геометрії. У 1828 році Мебіус опублікував мемуари"Баріцентричне числення", яке містило нові геометричні ідеї. Математик створив нову класифікацію поверхонь і кривих.
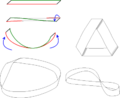
У 1858 році він запропонував односторонню поверхню, яка отримала назву листа або стрічки Мебіуса, яка відіграє велику роль у топології. Лист Мебіуса, розрізаний по середній лінії, перетворюється у поверхню, гомеоморфну поверхні циліндра. Розповідають, що відкрити односторонню повнрхню Мебіусу допомогла служниця, котра неправильно зшила кінці стрчок фартуха.
Стрі́чка Мьо́біуса чи Смужка (Лист) Мебіуса (німецька вимова [ˈmøbiʊs]) є поверхнею лише з однією стороною і лише однією границею. Вона має математичну властивість неорієнтованості. Також вона є лінійчатою поверхнею. Вона була незалежно відкрита німецькими математиками Мьобіусом і Лістінгом в 1858 році.
Її екземпляр легко може бути виготовлений зі смужки паперу, повертаючи один з її кінців на півоберту і з'єднуючи кінці стрічки для створення замкненої поверхні. Вевклідовому просторі є два типи стрічок Мьобіуса, в залежності від напряму здійсненого півоберту: за годинниковою стрілкою, та проти. Звідси можна зробити висновок, що стрічка Мебуіса є хіральною.
Стрічка Мьобіуса має цікаві властивості. Якщо спробувати розрізати стрічку по лінії, рівновіддаленій від країв, то замість двох стрічок Мьобіуса утвориться одна довга, двостороння, в два рази більш закручена стрічка. Якщо тепер цю стрічку ще раз так само розрізати, то утворяться дві стрічки, намотані одна на одну.
Підписатися на:
Дописи (Atom)